|
|
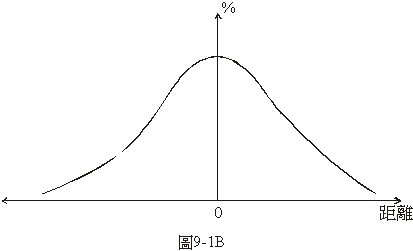
著點的平均位置之間的距離當橫座標,用在每一條的單位面積上彈著點數當縱座標畫成的曲線會像圖9-1B那樣:距中心近的小條上的彈著點密,距中心遠的小條上的彈著點稀。通常,像彈著點之類的散亂的分佈都會成為像圖9-1B中的曲線那樣的常態分佈(normal distribution)。
在五四的新文化運動中,推崇兩位「先生」,德先生和賽先生,德先生代表民主(democracy),賽先生代表科學(science),認為要救國必須推行民主與科學,還要打倒一位「差不多先生」,認為我們的國民凡事馬馬虎虎,差不多就好了,是中國積弱的一個主要的原因。若干年前在一個研討會中,我曾請教一群統計學的專家:德先生和賽先生當然應該推崇,但是差不多先生卻很冤枉,現在是不是到了該為他平反的時候了?
如果有人問:你的體重是多少?正確的回答方式應該是:差不多××公斤。因為雖然是自己的體重,我們並不真的知道準確的數字是多少。在磅秤上稱過之後,上一次廁所或是喝一杯咖啡甚至出了一點汗之後,體重就和秤的當時不一樣了。即使是正在磅秤上稱的時候,那一台磅秤的準確度也是很難說的。因此,在提到一個數目字時,前面加上差不多三個字,應該是一種負責任而比較科學的做法。再例如有人問我:你今天去上課,會有多少學生聽講?我會回答:差不多四十個。或是:大約四十個。因為在去上課之前我並不真的知道有多少學生會出席,選了這門課的同學,總難免有幾個因為各種原因不能來上課的,沒有選修這門課的同學也可能進來旁聽一下。再例如有人問:選修你這門課的有多少學生?我會回答:四十個。因為我手上有選課學生的名單,數過了,是四十個,不是三十九,也不是四十一,四十是一個我可以確定的數字。我們在談到體重之類的數字的時候往往會把「差不多」或「大約」的字略去,這樣也沒關係,因為聽的人一定有這方面的經驗,知道大家在講體重時,講的都是大約的數字。但在談到幾個學生來上課或幾個學生選課之類的數字時,如果我並不真的知道確切的答案,就應該在數字的前面加上「差不多」或「大約」的字樣。因為靠聽者的經驗他無法判斷你口中說出來的數字是一個估計出來的或是確切的答案。許多人與人之間不必要的誤會就是因為少用了「差不多」三個字而引起的。
由以上的幾個簡單的例子看,我們所遇到的數目字可以分成兩類:第一類是確定性的數字,譬如屋子裡有幾個人,盤子裡有幾粒花生米…等等,是可以一個一個地數得非常清楚,不可能有任何誤差的數目字。第二類是有若干不確定性的數字,是今天我們所討論的主題。再舉幾個例來說明:我們全國的人口是多少?人數是可以一個一個數得很清楚的,但是範圍大了數起來也很麻煩,而且經常有出生、死亡、出國、回國…等等的變化,數清楚了,過了幾分鐘之後又變了一些,因此通常只用一個大約的數字,如兩千一百萬,或兩千一百三十萬等等。我們在說兩千一百萬的時候,表示這個字,21,000,000,的有效數字是兩位,第一位的2是一定正確的,第二位的1便有很大的不確定性,第三位的0是介於+5和-5之間。因此,這個數字有介於20,500,000和21,500,000之間的不確定性。我們在說兩千一百三十萬的時候,表示這個數字,21,300,000,的有效數字是三位,第一位的2和第二位的1是一定正確的,第三位的3便有很大的不確定性,因此,這個數字有介於21,250,000和21,350,000之間的不確定性。我們在說兩千一百三十萬時,比說兩千一百萬時的準確度高了十倍。在說兩千一百三十萬時,表示這個數目字可能高估了五萬也可能低估了五萬;在說兩千一百萬時表示這個數目字可能高估了五十萬也可能低估了五十萬。在說一個有不確定性的數目字時,我們常常省略了「差不多」這三個字,而是用有效數字的多少來表示其可能差多少的不確定性。如果說的是一個三位有效數字,兩千一百三十萬的話,表示這個數字可能有上下五萬的誤差。如果自己沒有把握這數字的誤差在上下五萬之內的話,就不可以用三位的有效數字,就說兩千一百萬好了。這樣,只要正確的數字是在兩千零五十萬與兩千一百五十萬之間,別人都不可以說你的數字不正確。
如果我們到菜市場買一塊肉,價錢是每公斤100元,秤一下,這塊肉是1.25公斤,售價當然是125元。這一個賣肉用的秤的準確度,或是它秤得的有效數字只能到達小數點之後的第二位。換句話說,1.25公斤這個數字的最後一位,5,是不可靠的,這塊肉的重量是「差不多1.25公斤」或者是介於1.245公斤與1.255公斤之間。這一點差別,不論是賣肉的或是買肉的,誰佔了便宜或是吃了虧,大家都不介意,馬馬虎虎、差不多就可以了。如果買賣的不是肉而是黃金的話,當然就不能用這麼不準確的秤了。假如這筆交易是一公斤左右的黃金,每公斤的市價在五十萬元新台幣左右,就應該用一個準確度達到小數點以後第四位,十分之一公克,的秤。十分之一公克的黃金的價值在五十元左右。做了一筆五十萬元左右的大生意,因為秤的誤差,不論是賣主或買主,吃虧或佔便宜了二三十元,大家也都不會介意,馬馬虎虎、差不多就可以了。
在結婚喜筵的請帖上常寫:「下午六時三十分入席,請準時光臨」,有的寫成「下午六時三十一分入席,請準時光臨」。三十一分和三十分所差的這一分鐘的意義是什麼呢?發請帖的主人的用意是,如果寫六時三十分,6:30,的話,客人可能不把最後一個0當作有效數字,以為3才是最後一位的有效數字。這樣,在6:35分之前到的話就可以不算遲到。現在寫成六時三十一分,6:31,擺明了最後的有效數字是1,這樣,如果你在6時31.5之後才到就不能算「準時」了。這一招,最初一定是一位學過統計的想出來的,是否有效就因人因地而異了。
由以上的例子看,我們常把後面沒有其他數字的0不當作有效數字,例如表示兩千一百三十萬人口的21,300,000的後面的五個0事實上都不是有效數字。為了避免混淆,對於比較大的數字,例如台灣的人口,可以寫成:2.13×107,代表兩千一百三十萬,最後一位有效數字是3;也可以寫成2.130×107,也代表兩千一百三十萬,但這數字的準確度增加了十倍,因為最後多了一個0,這個0也是有效數字。一公斤多的肉,寫成1.25公斤,有效數字只到小數點後面的第二位;一公斤的黃金,寫成1.2500公斤,有效數字到小數點後的第四位,十分之一公克,這數字中最後的兩個零都是有效數字。
由以上的討論,各種量測用的工具,包括量重量的秤、量時間的碼錶、量長度的尺、…等等,都有一定的可信度或不可信度。例如那個菜市場裡肉攤上的秤,在小數點以後的第一位,十分之一公斤的那一位是可信的,小數點後的第二位就不很可靠了,上下有千分之五公斤的誤差(我這個例子舉得不是很好,因為肉攤上應該不需要這麼準確的秤)。每一種量測用的工具都會有誤差的,大家也都接受這一個不可避免的事實。誤差有兩種:一種叫做系統的誤差(systematic error),一種叫散亂的誤差(random error)。譬如那個肉攤上的秤,上面的刻度是每小格百分之一公斤,買賣的雙方在看指針的位置時都不耐煩看得很仔細,上下千分之五公斤,半格,的誤差是難免的。有時候多點、有時候少點,有時候佔點便宜、有時候吃點虧,長時間下來就誰也不吃虧了。這種誤差叫做散亂誤差,非常多次的散亂誤差的平均值是接近於零的。如果這位賣肉的老闆的這一個秤校正得不是很好,指針的位置總
是偏低一些,換句話說,總要放比1公斤多一點的肉上去它才會指到1公斤的刻度上。因為這個秤校正得不好,這位老闆每次都要多把一點點的肉給顧客。這種一面倒的誤差叫做系統誤差。系統誤差與散亂誤差之間是互相獨立的。在用這個校正得不太好的秤秤肉時,由於其他偶然的原因,還是有時候給得多一點、有時候給得少一點。少許的系統誤差和散亂誤差一樣很難避免,也是大家可以接受的。比較大的系統的誤差是可以避免的,譬如這位賣肉的老闆如果在每天開市之前,注意一下秤上沒有放東西時指針是否指在零點,放上一個標準的重量時,指針的位置是否正確就可以了。再例如我桌上有一把直尺,上面刻度的總長是30公分,最小的刻度是0.1公分,我用它來量一些東西時,因為眼睛看不太清楚所造成的散亂誤差應該在上下0.05公分之內。但是,我這把直尺到底有多標準呢?如果這把尺上的刻度與正確的長度相比之下有一些誤差的話,那麼我每次用它來量東西時,除了因為眼睛看不清楚所造成的散亂誤差以外,還都會有相同的系統誤差。如果我所量的長度非常重要,要求的準確度也非常高,不能允許有這麼大的系統誤差的話,就應該找一把更好的直尺或是其他更準確的測量長度的儀器。
我們在比較古老的故事書中都看到過不少神箭將軍的故事,例如:呂布轅門射戟,小李廣花榮梁山射雁,威廉鐵耳射小兒頭上的蘋果…等等。在新一些的故事書中也看過不少神槍手的故事。站在統計的立場看,這些英雄的箭術和槍法是否真的可能如此之神?如果我們把一枝長槍很穩固地固定在一個鐵架上,這個鐵架很重、很穩定,不可能因為子彈的發射而有任何的振動。從這枝長槍發射很多顆的子彈出去,打在100公尺以外的靶上,因為用的是固定得很好的同一把槍,已經消除了瞄準技術、槍法
和槍的性能的不同所造成的差異,這些子彈是否會落在靶上的同一個位置呢?事實上是不會的,而是分佈在一個平均位置的四週。每一個彈著點和它們的平均位置之間的距離就是所謂的散亂誤差,所瞄準的位置和彈著點的平均位置之間的距離就是這枝槍的系統誤差。一枝好槍,它的瞄準位置一定已經調節得與彈著點的平均位置非常接近,也就是說,系統誤差接近於零。彈著點為什麼會有散亂的誤差呢?因為每一粒子彈裡面裝的火藥的量、彈頭金屬的重量、形狀等等都不會絕對相等,一批好品質的子彈一定會盡可能做得完美,彈著點的散亂誤差就會很小,但總會有一些的。槍和子彈是如此,弓和箭也是如此,因此,呂布當年說他要一箭射中百步之外戟上的小枝,花榮說他要射中空中雁行中第三隻雁的頭部,所冒的風險是非常大的,小說家的筆總是會誇大些吧。
前面談過兩種最簡單的量測的工具-尺和秤,量測的結果都有一些不確定性。即使我桌上的直尺是一枝最標準的尺,因為上面的刻度很細,眼睛又不好,量一件東西的長度時難免有上下0.05公分的誤差。又談過弓箭和長槍,箭或子彈的實際落點與量測的落點,也就是靶的紅心,之間的距離總難免有些差距。現在,再談談賭博的工具。
賭博的方式很多,有的靠機智、反應、記憶和判斷力的成份很高,有的純靠運氣。任何方式的賭博都有若干靠運氣的成份,不然就不能稱其為賭博了。但有一些方式幾乎是純靠運氣的,最簡單的例子就是丟硬幣。拿一枚硬幣丟向空中,看它落地後是人頭或花的一面朝上而定輸贏。一般的硬幣都做得相當好,因此出現人頭或花的機率都大約是二分之一。在這裡用「相當好」、「大
約」等的字樣是因為一枚硬幣不可能做得絕對完美,出現人頭或花的機率也不可能正好是二分之一。到底有多麼的不完美,可以用非常多次的實驗來決定,用這枚硬幣丟非常多次,記錄出現人頭和花的次數,丟的次數愈多,所得到的結論愈可靠。如果你去賭丟硬幣的話,可以採用以下的策略:先觀察一段時間並且將結果記下來,譬如10,000次當中人頭出現了5083次,花出現了4917次,由這樣的記錄看來這枚硬幣做得相當好,但出現人頭的機率還是大一點。於是你開始下注,每次下1元都猜人頭,並且繼續記錄每次的結果,如果出現人頭的總數還是一直比出現花的總數多,表示最初10,000次的實驗次數夠多了,結論還算可靠,就繼續壓人頭;如果出現人頭的總數變得比花少了,表示實驗的總次數還是不夠多,這枚硬幣做得很完美,需要更多次的實驗,譬如100,000次才能得到結論,這時候你可以繼續賭下去,把每次1元的賭注永遠壓在出現總次數較多的花色上,這樣的賭法,這枚硬幣愈不完美,你贏的錢便愈多。假如上面所說的最初10,000次的結果相當正確的話,你壓了10,000次,大約可以贏一百多元;如果這枚硬幣很完美,你贏不到什麼錢但也不會輸什麼錢。這樣的賭法有一個重要的條件,就是你手上一定要有夠大的賭本,譬如身上有10,000元的賭本而每次只壓1元。如果每次壓1元但身上只有10元的賭本,或是有10,000元的賭本但因為你沈不住氣而每次壓1,000元的話,輸得光光只好回家的可能性就很大了。如果這枚硬幣是絕對完美的,每次壓1元,贏了就變成2元,輸了就變成0元,因此,當你壓下1元時就相當於花了1元買了一個機會或叫期望值。這個機會值多少錢呢?它值2×0.5+0×0.5=1元。這是一次極公平的賭博。如果用那枚你已經觀察了10,000次的硬幣,拿出1元壓人頭時,所買到的機會或期望值值多少錢呢?它值2×0.5083+0×0.4917=1.0166元。這對賭場或莊家當然較為不利而對你有利。這樣的賭法太理智了,幾乎沒有碰
運氣的成份,嚴格地說不能算是賭博了,賭場的經營者也不會歡迎你這樣的客人。對付你的方法很簡單,只要每丟100次換一枚新的硬幣,讓你的記錄資料失效就行了。
以上所舉的是一個最簡單的例,如果用幾枚硬幣而不是一枚,用六面的骰子而不是兩面的硬幣,或是用幾枚骰子,算起來就複雜太多了,但原則還是一樣的。作為一個賭客應該先在假定這些賭具都是完美的條件下,算一算每下1元的賭注所買到的機會或是期望值值多少錢?要比1元不要低得太多才行。美國的許多州都賣樂透彩卷,目的在支援教育,一共有多少獎項都清楚地印在彩卷上,誰都可以算得出來,每下1元的賭注買到的得獎期望值大約在0.3到0.4元的樣子。我們過去的愛國獎卷也差不多,也是把獎項和獎金印在背面,花1元的賭注,愛國的成份佔6至7角,發財的成份佔3至4角。香港的科技大學的經費聽說是靠賣馬票賺來的。一般民間的賭場與公營的彩卷正好相反,他們並不在輸贏的機率上佔賭客太多的便宜,靠的是:你口袋裡的賭本有限,他的資本近於無窮。
再回到用長槍打靶的問題。圖9-1A中的黑點代表靶上彈著點的位置,○代表這些彈著點的平均位置,╳代表所瞄準的位置。○與╳之間的距離代表這隻槍的系統誤差,如果是一隻好槍的話這個距離會非常小的。每一個彈著點和它們的平均位置間的距離代表這次射擊實驗的散亂誤差。如果射擊時槍身固定得非常牢固,由散亂誤差應該可以判斷生產這批子彈的品質管制是不是做得很好。
如果我們把靶的表面劃分成許多同心的圓條,每條的寬度都相同而且很小(在圖9-1A中只畫出了其中的一條),用每一條與彈
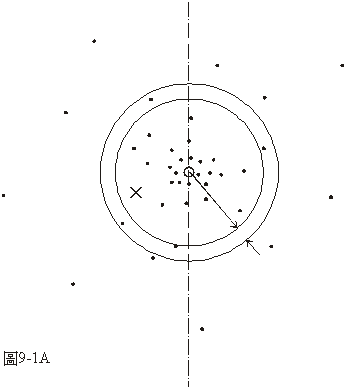
著點的平均位置之間的距離當橫座標,用在每一條的單位面積上彈著點數當縱座標畫成的曲線會像圖9-1B那樣:距中心近的小條上的彈著點密,距中心遠的小條上的彈著點稀。通常,像彈著點之類的散亂的分佈都會成為像圖9-1B中的曲線那樣的常態分佈(normal
distribution)。
所謂常態分佈,顧名思義就是一種很正常、很自然的分佈方式。離平均點近的地方彈著點當然會比較多,越遠的位置當然越少,就像圖9-1B的曲線所表示的那樣。許多自然界和社會上的現象都呈常態的分佈。下面舉幾個例:
一棵樹上結了許多蘋果,有的大些、有的小些,如果把每一個的重量都秤一下畫一個分佈曲線,結果大致上就會是像圖9-1B中的常態分佈曲線。如果把這一批蘋果加以挑選,分成大、中、小三級,大的可以賣貴些、小的賣便宜些,所分出來的每一級蘋果的重量的分佈曲線就不會是常態的像圖9-1B中的鐘形曲線了。常態分佈是一種很自然的分佈,一旦經過人工或機械的挑選就不那麼自然了。一個養雞場裡所生的蛋的大小、一群同年齡的男孩的體重或身高、一次考試的成績、…等等都應該大致上是常態的分佈。像今天我們談的問題,課後做一次考試,出來的成績會不會是常態分佈呢?不一定。因為同學中如果有幾位來自統計系或是修過統計學,他們都會拿滿分,分數的分佈就不會是常態的鐘形了。
再談一談體重的問題。身高比較高的體重當然應該重些。如果把體重的公斤數除以身高的公分數就可以把身高的因素消除了,所得的商較高的就比較胖些,較低的就比較瘦些。成年男人(或女人)的體重除以身高的商應該是常態分配的,如圖9-2。圖中
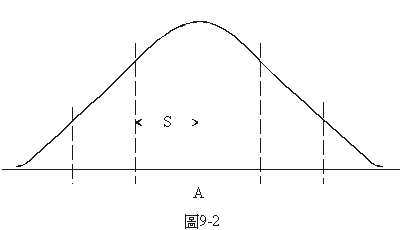
均值。在任何一個橫座標範圍內,曲線下面的面積就代表這個範的橫座標是體重除以身高的商,A點的位置是所有成年男人的平圍內人口的百分率。現在我們以A點為中心把曲線下面的面積分成等距離,S,的幾個區域。算一下你的體重除以身高的值,看它屬於那一個區域。如果落在A點左邊或右邊一個S的區域之內,你就不算胖也不算瘦;如果落在A點左邊一個S以外,你就是一個瘦子;如果落在A點右邊一個S以外,你就是一個胖子;如果落在A點左邊兩個S以外或是右邊兩個S以外,你就是嚴重地瘦或胖,需要找醫生去談談了。
到了選舉的時候,在正常的情況下,選民對一些政治議題的意見應該也屬於像圖9-3中的常態分配。圖中A、B、C、D的位置代表四個候選人對這一個議題的立場。由這個圖看來,A點右方的全部選民會把票投給A,但可惜在這個區域內曲線下面的面積很小,表示選民的人數很少;在A的左邊B的右邊等距離處畫了一條虛線,在這虛線右邊的選民應該會把票投給A,左邊的選民則投給B,這虛線雖然與A、B等距離,但曲線下面的面積是B那一邊的較大;依同樣的原則B與C分得他們的立場之間
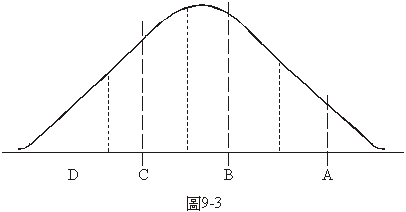
的選民的票,C與D分得他們之間的票,D得到立場在他本身的左方的所有選民的票。由曲線下面的面積看,得票最多的候選人應該是B,實際的選舉當然不是這麼簡單,但候選人爭取選票的策略的基本原則大約也不過如此。
有一個公司生產一種瓶裝的飲料。瓶上標示的含量是500c.c.。政府的檢驗單位為了保障消費者的權益常會抽樣檢查,因為體諒裝瓶的機器難免有些誤差,所以規定檢查的結果在490c.c.以上時不于追究,但如果在490c.c.以下就要罰款。這公司有一種裝瓶機,裝到瓶中飲料的量的分散狀況如圖9-4A。如果把這機器設定在每瓶裝500c.c.,那麼瓶中裝進去的飲料的量的分佈的情形就像這圖中曲線下的面積一樣,有一半比500c.c.多,另一半比500c.c.少,平均起來是每瓶500c.c.。這樣,這公司並沒有欺騙顧客,但由圖9-4A看,瓶中飲料含量少於490c.c.的機率相當大,被檢驗出來罰款的風險也不小。於是考量的結果,把這機器改設定在每瓶裝505c.c.,如圖9-4B所示。這樣瓶中飲料含量少於490c.c.的機會就小得多了,可以省下不少罰款,但每瓶平均要多裝5c.c.的飲料,當然要多花這麼多原料的成本。如果這個公司所生產的飲料的原料成本低,被查到含量少於490c.c.後的罰金也
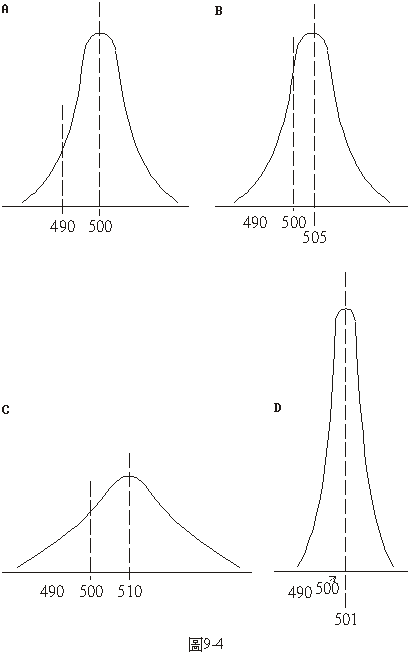
不是很高,但裝瓶機的價格卻很昂貴,是不是就應該買價格便宜而誤差大些的裝瓶機?這台機器裝到瓶中的飲料的量的分佈情形如圖9-4C,散亂的誤差相當大。因為飲料反正很便宜,可以把機器設定在每瓶的平均裝填量為510c.c.,雖然如此,因為瓶中飲料含量小於490c.c.的機率仍然不是很小,但為了節省在設備上的投資,花些罰金仍是划得來的。如果這公司生產的是一種原料成本非常高的飲料,被查到瓶中含量少於490c.c.後的罰金也很高,就應該多花些設備上的投資買更精密的裝瓶機。這樣一台機器裝到瓶中的飲料量的分佈情形如圖9-4D,散亂誤差相當小,把每瓶的平均裝填量設定在501c.c.就可以使因為裝填量小於490c.c.而付罰金的機率降到很小。這樣,多花了設備費而節省了原料成本和罰金,算起來仍是划得來的。由以上的討論看來,這個賣飲料的公司如果有了政府檢驗頻率和罰款辦法的資料、各種裝瓶機價格和性能或散亂誤差的資料、以及原料價格的資料,便可以規劃最有利的生產策略。
從飛機上看海面的浪,大浪、小浪,大浪的上面有小浪,小浪的上面有更小的浪,一直到毛細現象的小波,真是複雜,理論上如何處理呢?天氣的變化、地震何時發生、股票的漲跌…能否準確地預測呢?站在台北火車站前的陸橋上看看下面熙熙攘攘的人潮,有的過得很幸福、有的辛苦,為什麼有這麼大的差別呢?如果說:這是命運、是前生注定的,這樣的說法實際上等於說:不知道或是不想知道。有因必有果、有果必也有因,但因果之間錯綜複雜很難理清。就連用長槍打靶,瞄準了紅心卻打偏了很多,這麼簡單的問題我們都很難理清其中的因果關係。怎麼辦呢?求助於統計吧。統計學是一門很有趣的學問,可以幫我們找出一些亂中之序。